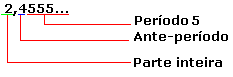Fração geratriz

   
Conforme você já estudou, todo número racional (Conjunto Q), resulta da divisão de dois número inteiros, a divisão pode resultar em um número inteiro ou decimal.
Convém lembrar que temos decimais exato.
Exemplo: 2,45;  0,256;   12,5689;    12,5689

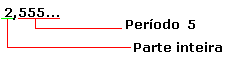
Temos também decimais não exato (dízima periódica)
Exemplo: 2,555555…. ; 45,252525….;  0,123123123…;   456,12454545;  7,4689999….

Você deve saber, que em uma dízima periódica a parte decimal que repete, recebe o nome de período, a parte que não repete é chamada de ante-período, a parte não decimal é a parte inteira.
Exemplo:

Dízima periódica composta	Dízima periódica simples

   
Dízima periódica simples:

Devemos adicionar a parte decimal à parte inteira. Devemos lembra que a parte decimal será transformada em uma fração cujo numerador é o período da dízima e o denominador é um número formado por tantos noves quantos
sãos os algarismos do período.

   
Exemplos:

   
Dízima periódica composta:

Devemos adicionar à parte inteira uma fração cujo numerador é formado pelo ante-período, seguindo de um período, menos o ante-período, e cujo denominador é formado de tantos noves quantos são os algarismos do período
seguidos de tantos zeros quanto são os algarismos do ante-período. 

   
Exemplos: