Frações
|
Frações O símbolo Chamamos: Se a é múltiplo de b, então a fração Veja um exemplo: O significado de uma fração Uma fração envolve a seguinte idéia: dividir algo em partes iguais. Dentre essas partes, consideramos uma Exemplo: Aline comeu
Na figura acima, as partes pintadas seriam as partes comidas por Aline, e a parte branca é a parte que sobrou do bolo. Como se lê uma fração As frações recebem nomes especiais quando os denominadores são 2, 3, 4, 5, 6, 7, 8, 9 e também quando os denominadores são 10, 100, 1000, …
Como Podem Ser As Frações
São frações que representam uma quantidade menor que o inteiro, ou seja representa parte do inteiro. Exemplos: Frações Impróprias São frações que representam uma quantidade maior que o inteiro, ou seja representa uma unidade mais parte dela. Exemplos: Frações Aparentes São frações que representam uma unidade, duas unidades etc. Exemplos: Frações Equivalentes Duas ou mais frações que representam a mesma quantidade da unidade são equivalentes. Exemplos: Simplificando Frações Quando multiplicamos ou dividimos o numerador e o denominador de uma fração pelo mesmo número, Exemplos: Reduzindo Frações ao Mesmo Denominador Exemplo: Adição e Subtração de Frações
Para subtrair frações com denominadores iguais, basta subtrair os numeradores e conservar o denominador. Exemplos:
Denominadores diferentes Para somar frações com denominadores diferentes, devemos reduzir as frações ao menor denominador comum e, em seguida, adicionar ou subtrair as frações equivalentes às frações dadas. Para obtermos estas frações equivalentes Exemplo: Vamos somar as frações
Multiplicação e Divisão de Frações Multiplicação 1º Caso Multiplicando um número natural por uma fração Na multiplicação de um número natural por uma fração, multiplicamos o número natural pelo numerador da fração e conservamos o denominador. Exemplos:
Multiplicando Fração por Fração Na multiplicação de números fracionários, devemos multiplicar numerador por numerador, e denominador por denominador. Exemplos:
Divisão Exemplos:
Potenciação e radiciação de números fracionários Potenciação Na potenciação, quando elevamos um número fracionário a um determinado expoente, estamos elevando o numerador e o denominador a esse expoente: Exemplos:
Radiciação Exemplos:
|


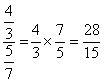
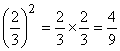
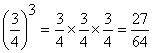
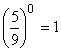

Seja o primeiro a comentar!